三文读懂PCA和PCoA?
今天看到金唯智公众号的推文《三文读懂PCA和PCoA》(《一》,《二》,《三》)。作者以平民化的语言,剔除数学术语,介绍了二者的区别,是很好的尝试,但是文中提出的很多关键性总结,都存在着明显的漏洞。
特别指出在第二篇文章中:
- “PCA基于物种丰度矩阵就意味着PCA分析的矩阵维度是就等于物种数目。换句话说,你要分析的样本如果要做PCA分析,那么一般来说有多少个物种就有多少个维度”。
既然说到丰度,那有一个很容易忽视的点,就是所有物种丰度相加为常数(1或100%),所以说数据的维数其实是物种数-1。而相对丰度其实并不在传统意义的欧式空间中(参见Aitchison的《The Statistical Analysis of Compositional Data》)。PCA涉及到的变换其实是会保持数据点之间欧式距离不变(考虑所有PC的话),那么PCA分析是否适用于丰度(成分)数据,是一个存在争议的课题(参见Aitchison的《Principal Component Analysis of Compositional Data》)。所以在成分数据(测序数据,特别是microbiome)数据的时候,我们常采用一些生态距离,然后做PCoA。
- “同样的道理,PCoA基于样本间的距离矩阵就意味着PCoA分析的矩阵维度与样本数目相关。如果你要分析的样本做PCoA分析的话,那么一般来说有n个样本就至多有n-1个维度”。
这是一个n(样本数目)和p(维度)的问题,维度就是维度,p就是p,不能混淆。
- “多数情况下,我们在做降维处理的时候,期望维数越低越好,这样我们就可以最大程度地保真原始数据”
天下没有免费的午餐,维数越低,保真度自然越低。而PCA、PCoA所做的是在低维空间中尽量多的保存数据之间的差异。
- “如果样本数目比较多,而物种数目比较少,那肯定首选PCA;如果样本数目比较少,而物种数目比较多,那肯定首选PCoA”
这是一个很有意思的问题,其实PCoA和PCA的结果取决于PCoA的实现,但是直觉上想,既然PCA的变换会保存数据点间的欧氏距离,那么它和基于欧式距离的PCoA有什么区别呢?
下面做一个实验,我们用两组数据(样本数目>维度,纬度>样本数目)来看看R中常见的PCA和PCoA实现的结果有何不同。
iris:样本数目>维度
## Low dimensional data (n>>p)
data(iris)
par(mfrow=c(2,2),cex=0.7, pch=19)
## PCA
pca <- prcomp(iris[,-5])
plot(pca$x[,1:2], col=iris[,5], xlab='PC1',ylab='PC2', main='PCA')
## PCoA
pcoa <- cmdscale(dist(iris[,-5], method = "euclidean"))
plot(pcoa, xlab='MDS1',ylab='MDS2', col=iris[,5], main='PCoA')
## pairwise distances
plot(as.vector(dist(pca$x[,1:2])), as.vector(dist(pcoa)),
xlab='PCA', ylab='PCoA', main='Pairwise distances',
pch=19, col=rgb(0,0,0,0.3), cex=0.5)
plot(as.vector(dist(pca$x[,1:2])) - as.vector(dist(pcoa)),
main='Difference in pairwise distances', ylab='Delta',
cex=0.5, col=rgb(0,0,0,0.3))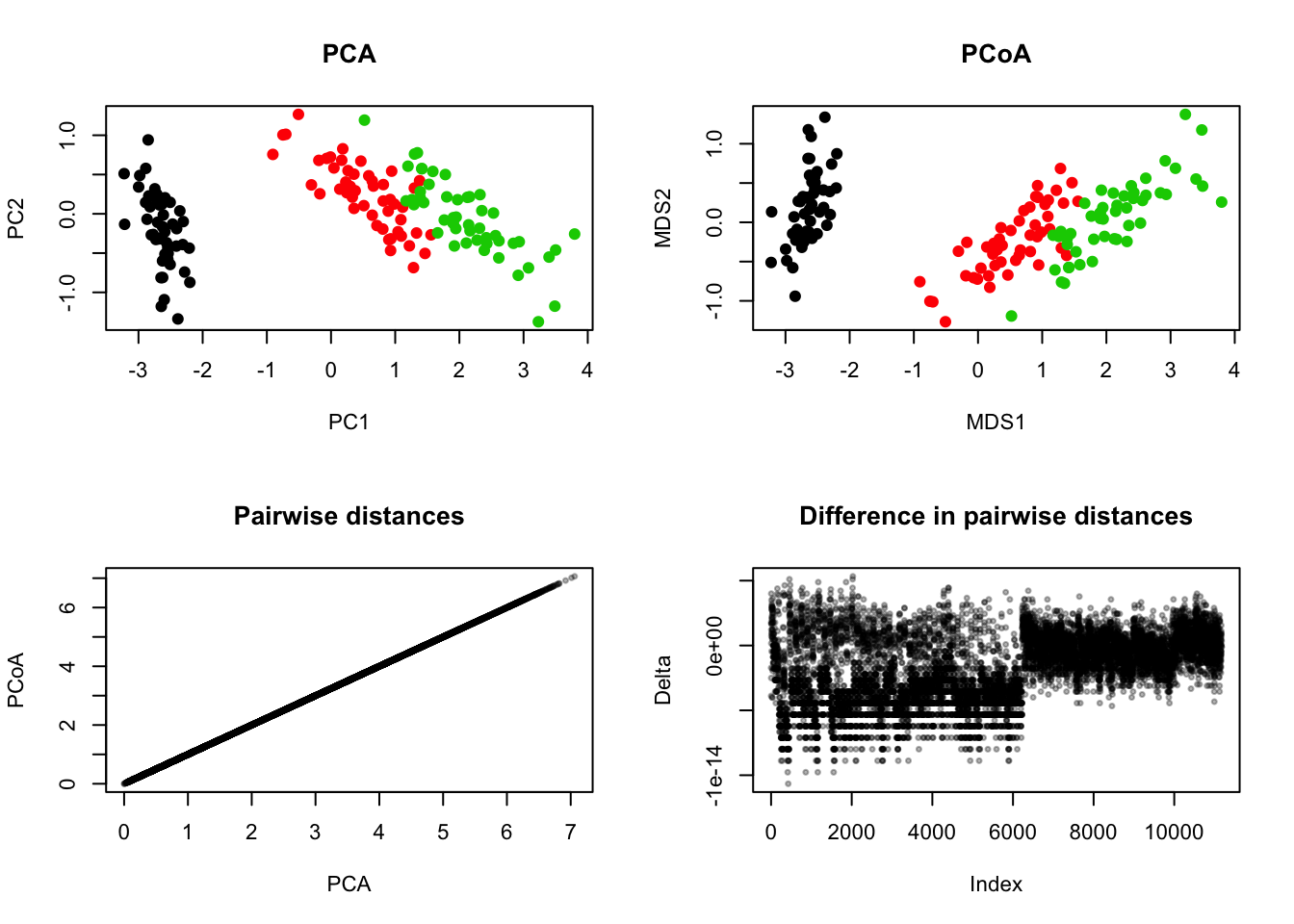
Gene expression dataset:维度>样本数目
## High dimensional data (p>>n)
## source("http://bioconductor.org/biocLite.R")
## biocLite("hopach")
suppressMessages(library(hopach))
par(mfrow=c(2,2),cex=0.7, pch=19)
data(golub)
pca <- prcomp(t(golub))
plot(pca$x[,1:2], col=golub.cl+1, xlab='PC1',ylab='PC2', main='PCA')
pcoa <- cmdscale(dist(t(golub), method = "euclidean"))
plot(pcoa, xlab='MDS1',ylab='MDS2', col=golub.cl+1, main='PCoA')
plot(as.vector(dist(pca$x[,1:2])), as.vector(dist(pcoa)),
xlab='PCA', ylab='PCoA', main='Pairwise distances',
pch=19, col=rgb(0,0,0,0.3), cex=0.5)
plot(as.vector(dist(pca$x[,1:2])) - as.vector(dist(pcoa)),
main='Difference in pairwise distances', ylab='Delta',
cex=0.5, col=rgb(0,0,0,0.3))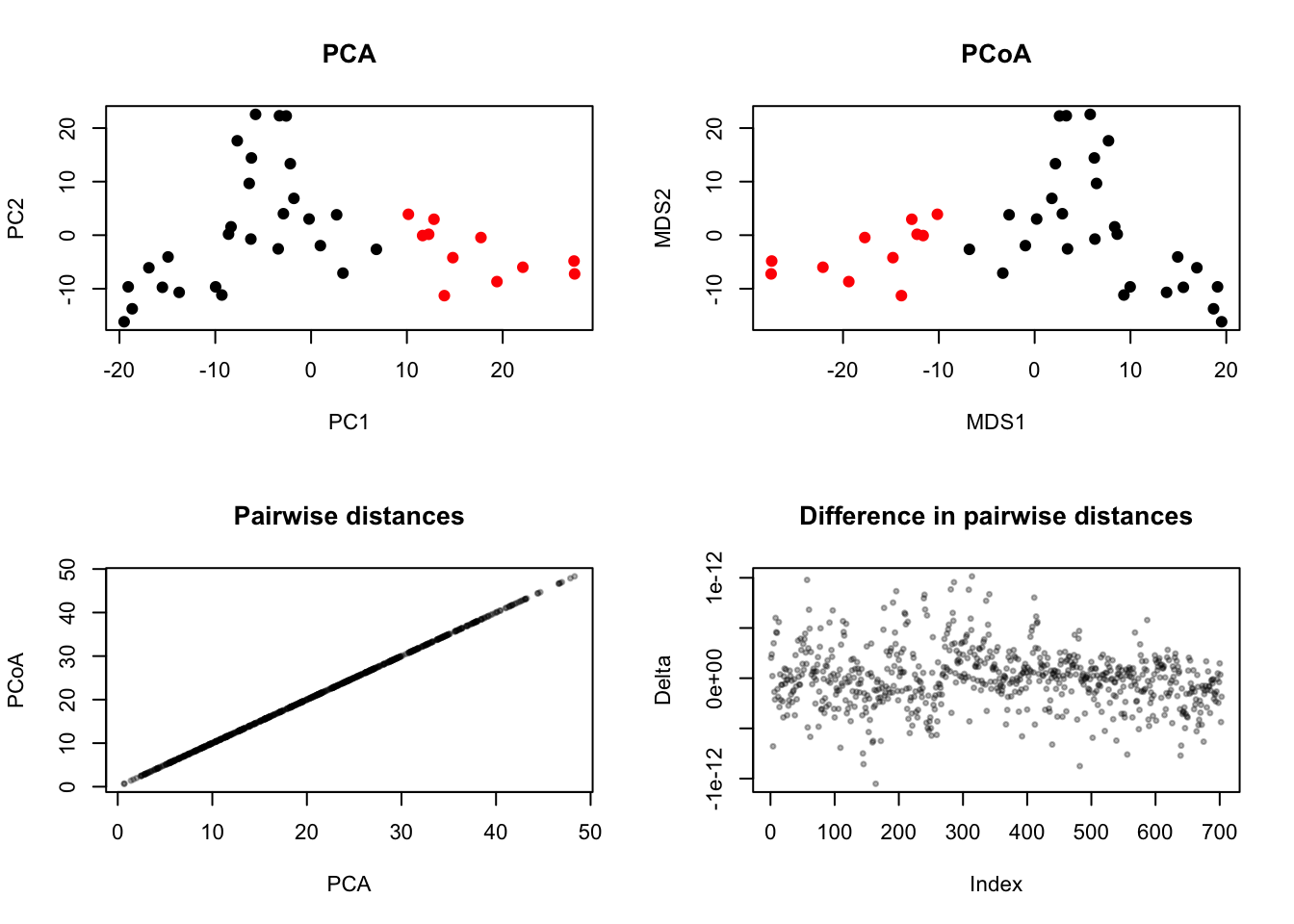
很明显,在基于欧氏距离的cmdscale和PCA在前两个维度上并没有什么区别。我个人一度以为PCA和基于欧式距离的PCoA其实是等同的,但是后来我们在一些PCoA的实现中确实看到了和PCA结果的差异,但是其实这个差异并不是很大。网上其实有很多的讨论,比如这个。