成分之咒与ReBoot算法

Jan 12, 2018 2 min read R

写在前面

本文的大部分内容都来自我们之前的一篇综述文章Li et al, 2016。

微生物组测序与成分数据

微生物组测序数据的获得其实有很多抽样过程（Sampling process）存在，比如说，粪便微生物组其实是对肠道微生物的一次抽样，测序的过程也是对所有DNA分子的一次抽样。最后，我们得到的OTU表中的OTU read count与测序深度相关，很显然测序深度是一个技术上的干扰因子（confounder），所以我们要对OTU表进行标准化（Normalization）。最简单的标准化方法，就是用read count除以样本内所有OTU的read count之和，获得每个OTU的相对丰度（relative abundance）。这种只有相对丰度的数据（相加总数为常数1或100）被称为成分数据（Compositional data）。你可能注意到，作为成分数据一种的微生物组的数据中缺乏一个重要的信息–微生物总量（total abundance）。

成分之咒（Curse of compositionality）

（一些推导的废话可以跳过）

成分数据会对一些列统计分析产生影响，最典型的就是计算相关系数（correlation）。其中Pearson相关系数\(\rho_{X,Y}\)是由协方差矩阵算出来的，对于两个OTU的数量（由随机变量\(X\)，\(Y\)表示），相关系数可以按下面公式计算（详细解释见维基百科）：

\[COV(X, Y)=E[(X-E[X])(Y-E[Y])]\]

\[\rho_{X,Y}=\frac{COV(X,Y)}{\sqrt{COV(X,X)\times COV(Y,Y)}}\]

其中\(COV(X,X)\)其实就是\(X\)的方差。其中根据协方差的性质我们可以得出成分数据的协方差性质：

\[\sum_{i=1}^px_i=1 \Rightarrow \sum_{i=1,i\neq r}^pCOV(x_i, x_r)=-COV(x_r, x_r)\]

我们知道方差（\(COV(x_r, x_r)\)）一定为正值，所以成分数据的协方差（同理相关系数）天然趋向于负值！

天然的负相关

上面的公式推导，其实简单的想一想，因为相加为1，所以一个OTU相对丰度增加，其他OTU必然减少，所以本来不相关的OTU数量在转化为成分数据后也会有负相关的趋势，也就是我们常见的微生物组领域所说的Compositional effect或Compositional bias。以下为简单的一个实验，Species 1和Speacies 2本来不相关，但是其相对丰度负相关：

## 加载r包
library(ggplot2)
library(reshape2)
library(cowplot)

## ggplot主题配置
figtheme <- theme_bw() + theme(text = element_text(size=10,face='bold'),panel.border  = element_rect(colour = "black",size=2))
theme_set(figtheme)

## 随机产生独立的5个OTU绝对数量 
means <- c(400,300,95,90,85)
data <- sapply(means, function(x) rnorm(100, x, x*0.05))
colnames(data) <- c('Species1', 'Species2','Species3','Species4','Species5')

## 绝对数量的画图
data.long <- melt(data)
colnames(data.long) <- c('Sample','Species','Abundances')
p1 <- ggplot(data.long, aes(x=Sample, y=Abundances, group=Species, color=Species)) + geom_line(size=1) + labs(y='Absolute Abundance')
p2 <- ggplot(data.frame(data), aes(x=Species1, y=Species2)) + geom_smooth(se=F,size=2,col='cyan') + geom_point(alpha = .7, size=2, col='darkblue')  + labs(title='Absolute Abundances',x='Species 1', y='Species 2')

## 相对丰度
data.norm <- t(apply(data, 1, function(x) x/sum(x)))
data.norm.long <- melt(data.norm)
colnames(data.norm.long) <- c('Sample','Species','Abundances')
p3 <- ggplot(data.frame(data.norm), aes(x=Species1, y=Species2)) + geom_smooth(se=F,size=2,col='pink') + geom_point(alpha = .7, size=2, col='darkred') + labs(title='Relative Abundances',x='Species 1', y='Species 2')

plot_grid(p1,plot_grid(p2,p3, nrow=1), ncol=1)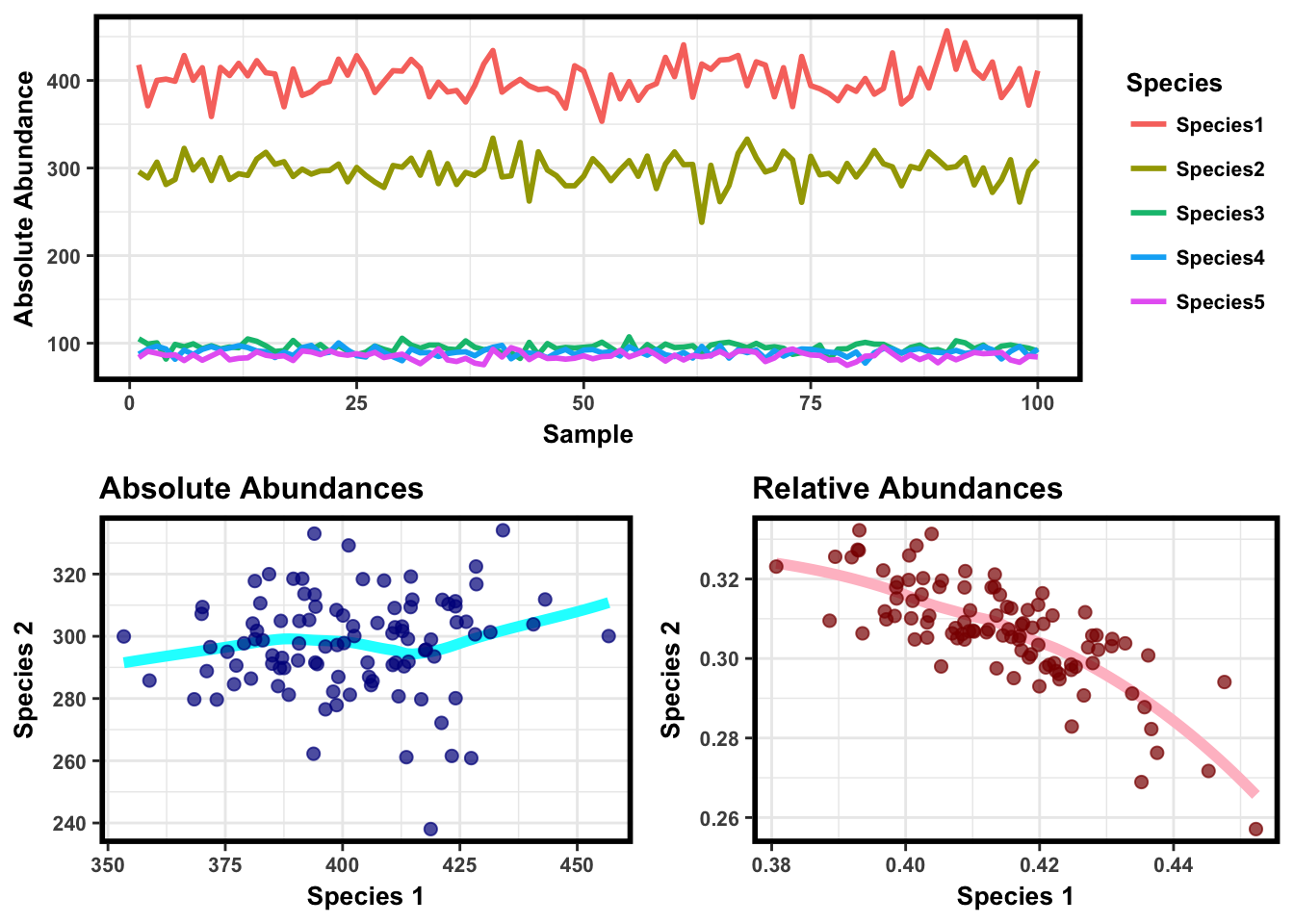

成分之咒（Curse of compositionality）这个词出现于今年发表于Nature Biotechnology的一篇综述文章，讲的就是成分数据对相关系数的影响。我所阅读到最早在微生物组领域提出这个问题，并给出解决算法的两篇文章（Faust et al, Friedman et al）都来自2012年的PLOS Computational Biology。这两篇文章可能你没有读过，但是他们都演化成了很有名的工具，前者就是R包CCREPE和Cytoscape插件CoNet，后者就是SparCC。

CCREPE的ReBoot算法

注：这里先介绍CCREPE算法，并不是因为它是最好的算法，只是因为它算法简单，同样用这个算法来演示下载、清洗、可视化数据。

大佬Curtis Huttenhower的ReBoot想法很简单，对于一个OTU表，我们把每一个OTU在不同样本中的数量打乱，这样所有的OTU数量都独立而不应该相关，之后我们从新标准化到相对丰度，然后计算相关系数，所有的非0相关系数都是由于标准化导致的假阳性（False positive）。这样的过程可以重复N次，然后我们就得到了每一对OTU的相关系数的一个零分布（Null distribution）。然后我们用原始的数据计算出的相关系数跟这个零分布比较一下，就可以获得p值，显著的p值才是真正相关的（其中的bootstrap算法跟成分数据关系不大，所以在次略过）。

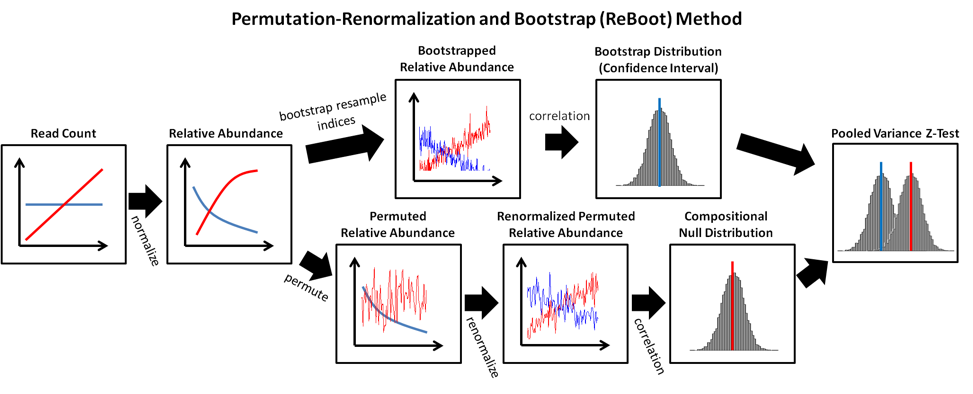
ReBoot算法

使用CCREPE计算相关系数

安装CCREPE：

source("https://bioconductor.org/biocLite.R")
biocLite("ccrepe")

下载并解压HMP 16S数据和元数据（以下认为保存于“~/Downloads/”），然后进行数据预处理：

## 使用data.table包快速读取大数据
library(data.table)
library(tidyverse)
## 元数据
metadata <- fread('~/Downloads/v35_map_uniquebyPSN.txt')
## 选出唾液数据并去掉唾液中不存在的OTU
IDs <- c('#OTU ID', as.character((metadata %>% filter(HMPbodysubsite=='Saliva'))[,1]))
otutab <- data.frame(fread('~/Downloads/otu_table_psn_v35.txt',head=TRUE, select=IDs,sep='\t') %>% 
    filter(rowSums(.[,-1])>0), 
    row.names = 1
    )

## Warning in fread("~/Downloads/otu_table_psn_v35.txt", head = TRUE, select
## = IDs, : Starting data input on line 2 and discarding line 1 because it has
## too few or too many items to be column names or data: # QIIME v1.3.0-dev
## OTU table

## Warning in fread("~/Downloads/otu_table_psn_v35.txt", head = TRUE, select
## = IDs, : Column name '700038483' not found in column name header (case
## sensitive), skipping.

## Warning in fread("~/Downloads/otu_table_psn_v35.txt", head = TRUE, select
## = IDs, : Column name '700038903' not found in column name header (case
## sensitive), skipping.

## 
Read 66.1% of 45383 rows
Read 45383 rows and 291 (of 4790) columns from 0.409 GB file in 00:00:04

## 筛选数据
otutab.fil <- otutab %>% select(which(colSums(otutab)> 3000 )) %>% ## 样本筛选：样本read总数超过2000
                     filter(rowSums(.>1) > NCOL(.)*0.8)## OTU筛选：超过1个read的样本数量在90%以上
## 得到30个OTU，215个样本

## 标准化成relative abundance
otutab.fil.norm <- apply(otutab.fil, 2, function(x)x/sum(x))

使用CCREPE来计算Co-occurence网络，使用Spearman相关系数：

library(ccrepe)
ccrepe.res <- ccrepe(x=t(otutab.fil.norm))

结果有4部分：

p.value：ReBoot测试p值
z.stat：Z-score
sim.score：计算出的相关系数，默认值为Spearman相关系数
q.value：FDR修正过的p值

我们需要的是q.value和sim.score。

可视化：

library(igraph)

## 根据q值过滤Co-occurrence矩阵
mat <- ccrepe.res$sim.score
mat[ccrepe.res$q.values > 1e-5] <- 0 ## q值不小于1e-5的correlation设为0
## 导入igraph
g <- graph_from_adjacency_matrix(adjmatrix=mat, mode=c('undirected'), weighted = TRUE, diag = FALSE)
## 去掉没有边的节点
g <- delete.vertices(g, V(g)[degree(g)==0])
## 根据correlation方向上色
E(g)$color <- ifelse(E(g)$weight>0, 'green', 'red')
## 根据correlation值设置边的粗细
E(g)$width <-  abs(E(g)$weight) * 5
plot(g, layout=layout_with_lgl(g), edge.curved=.3)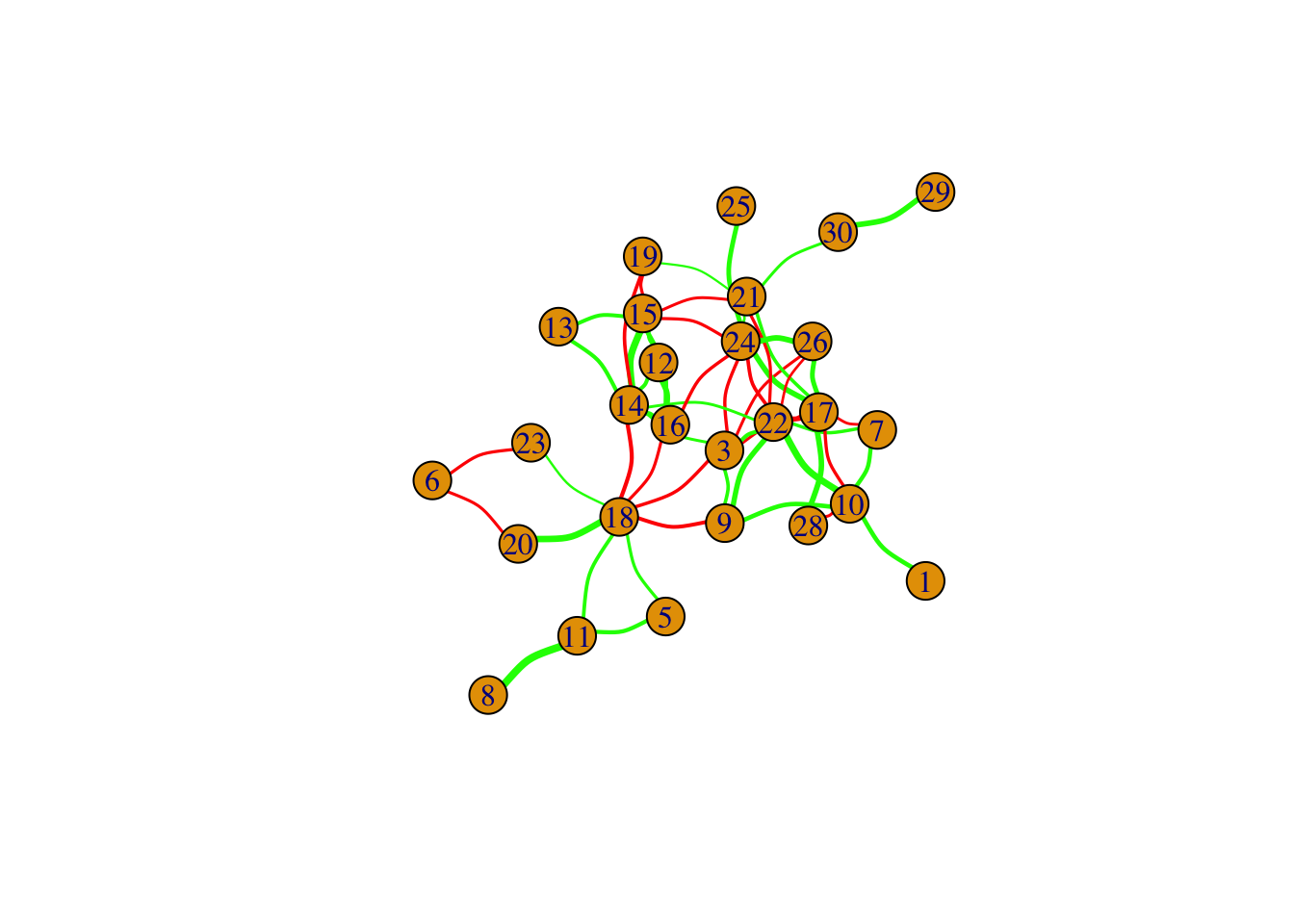

写在后面

画图完成了，剩下的就是进行生物学的解读了，比如算出这个网络有什么特征等等。但是自己想特别说一下，在上面的网络中，使用CCREPE的sim.score的正负和绝对值其实不是很有意义，因为sim.score其实就是Spearman相关系数，虽然我们删去了可能由于成分数据特征造成的假阳性，但是对于这些保留下来的相关系数如何处理，CCREPE其实并没有操作，所以在解读时一定要小心。另外记得之前看到一篇文章说（找不到了），很多人喜欢在微生物组的文章里画这么一个Co-occurence网络图，但是并没有进行解读，只是为了“See! We can do system biology!”。所以还是说，即使是数据导向的组学，“套路”的时候也要清楚知道自己做的是什么，为什么（不）可以这样做，回答了什么样的生物学问题。

R Microbiome